概述

TreeMap在实际的开发以及面试中比较少见。一般用到/面试提到TreeMap的场景大概率是

1. 需要排序（自然顺序或者指定顺序）同时还需要去重可以选择的一个集合。
2. 性能问题，问你TreeMap的get put contains等方法的时间复杂度（本质还是考的内部的数据结构）

Java TreeMap实现了SortedMap接口，也就是说会按照key的大小顺序对Map中的元素进行排序，key大小的评判可以通过其本身的自然顺序(natural ordering)，也可以通过构造时传入的比较器(Comparator)。

TreeMap底层通过红黑树(Red-Black tree)实现，也就意味着containsKey(), get(), put(), remove()都有着log(n)的时间复杂度

树的基础知识

在说红黑树之前，我们需要先简单复习下树的数据结构。树是非常重要且常用的一种结构，对于算法和数据处理有着重要的作用。

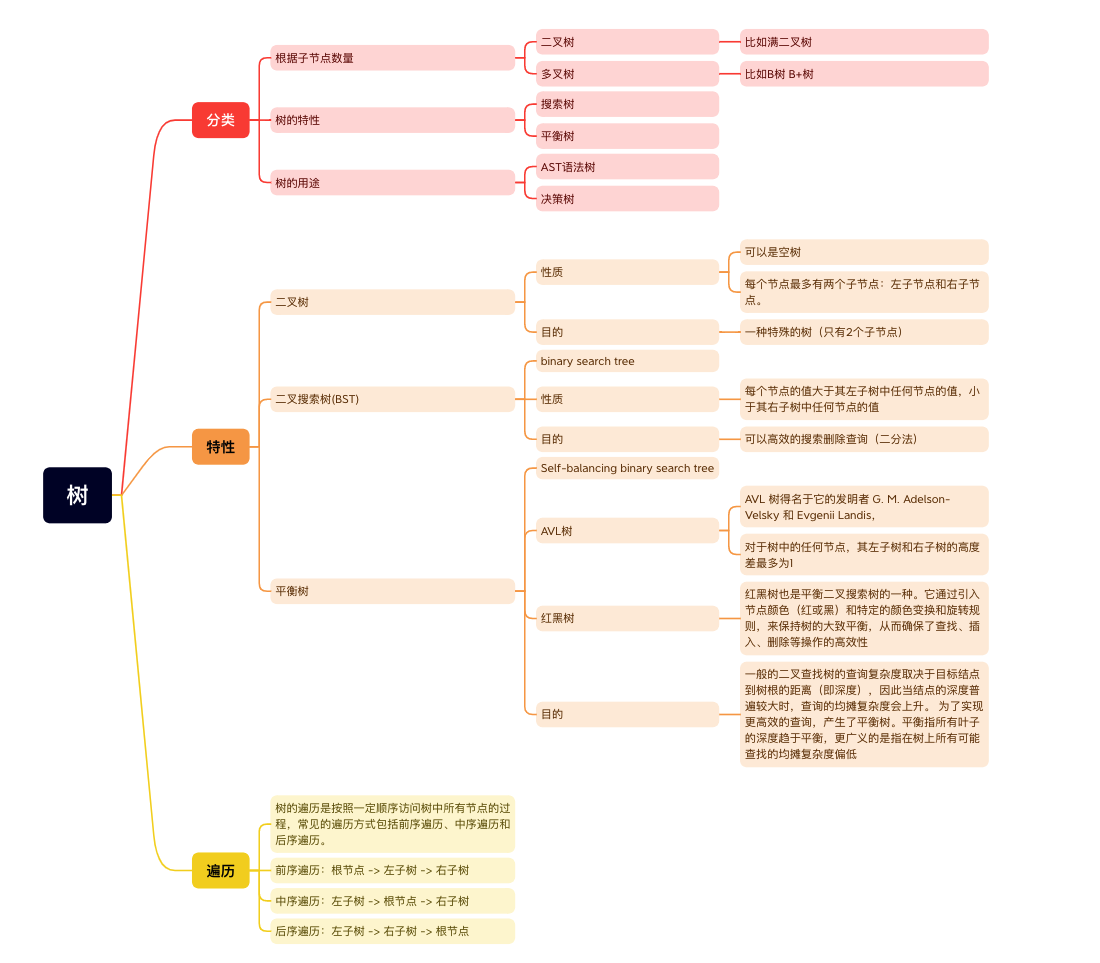
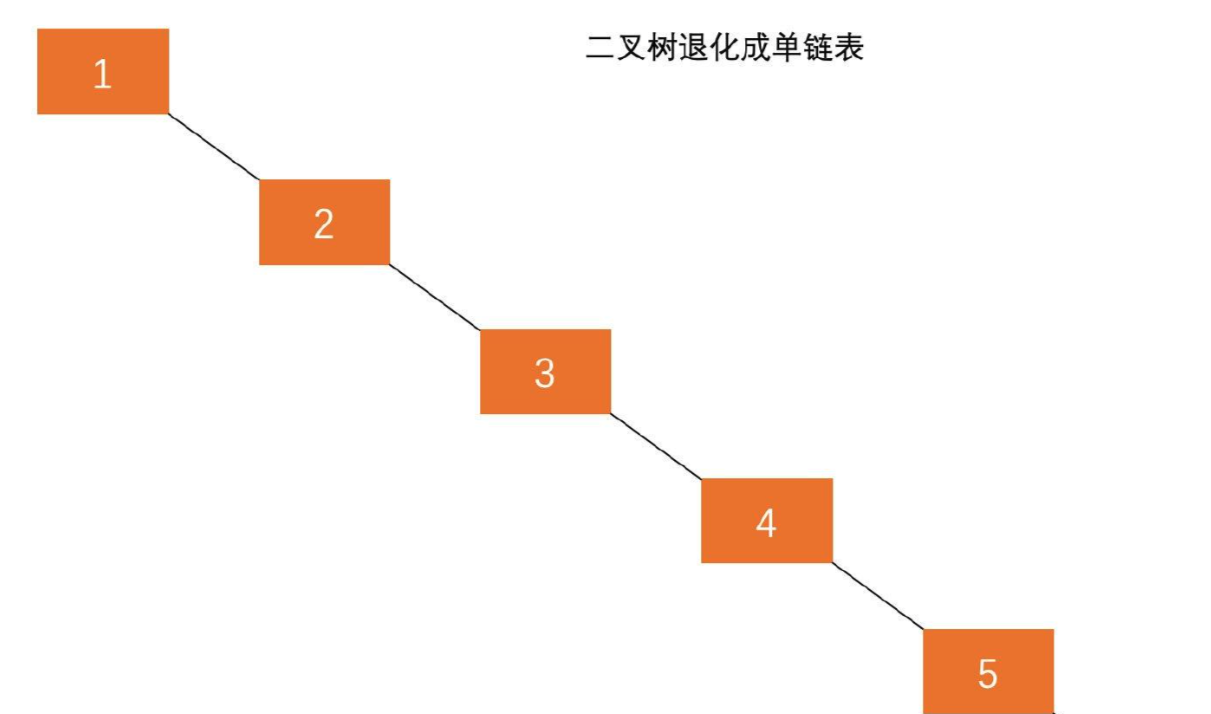
在二叉查找树中，当插入和删除操作不断进行时，树可能会变得不平衡，这就导致了查找效率的下降。最糟糕的情况下，二叉查找树可能退化为链表，这就使得查找操作的时间复杂度从平均情况的O(logn)变为最糟糕情况的O(n)。

为了解决这个问题，人们发明了自平衡二叉查找树，其中一种就是红黑树。红黑树通过引入额外的规则（红黑性质）来保持树的平衡（这5个特性需要牢记)：

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 所有叶子节点（NIL）是黑色。
4. 如果一个节点是红色的，则它的两个子节点都是黑色的。
5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

这些规则确保了最长的可能路径（红黑路径）最多是最短的可能路径（全黑路径）的两倍长。换句话说，红黑树是近似平衡的，这意味着任何查找路径的长度都不会超过其他路径的两倍，从而保证了查找、插入和删除操作的时间复杂度为O*(logn)。

总的来说，红黑树的出现是为了解决二叉查找树在最坏情况下性能下降的问题，通过保持树的大致平衡来提供一致的性能。

下面我们就来看下 红黑树是通过何种方式来解决问题的。

红黑树的操作（大概知道即可）

这部分的内容是作为深入讲解的，大部分同学知道即可，真的感兴趣的可以结合以下内容自己写一个红黑树或者debug代码增加理解。

左旋

红黑树的基本操作是添加和删除，在对红黑树进行添加和删除之后，都会用到旋转方法，为什么呢？道理很简单，因为添加或者删除红黑树中的节点之后，红黑树就发生了变化，可能不满足上面的5条性质了，这个时候就需要通过旋转操作来保证它依旧是一棵红黑树，旋转分为左旋和右旋（旋转操作仅仅只是用来调节节点的位置的，就是为了满足红黑树的性质5）

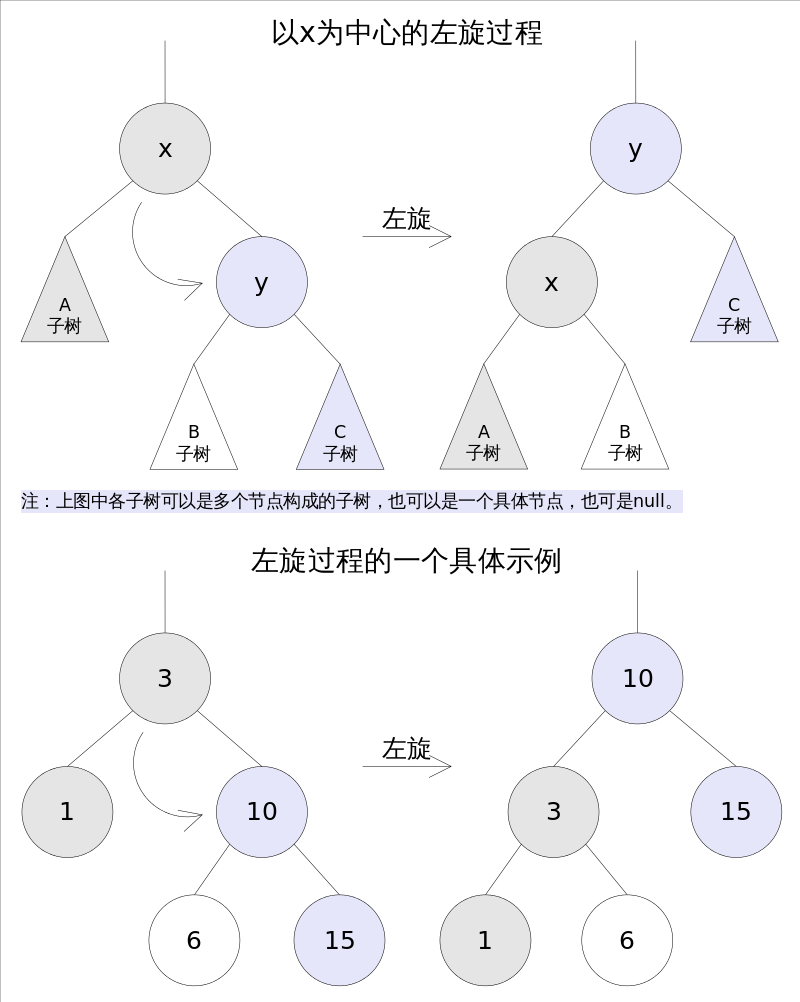
左旋是将X的右子树绕X逆时针旋转，使得X的右子树成为X的父亲，同时修改相关节点的引用，旋转之后，要求二叉查找树的属性依然满足

右旋

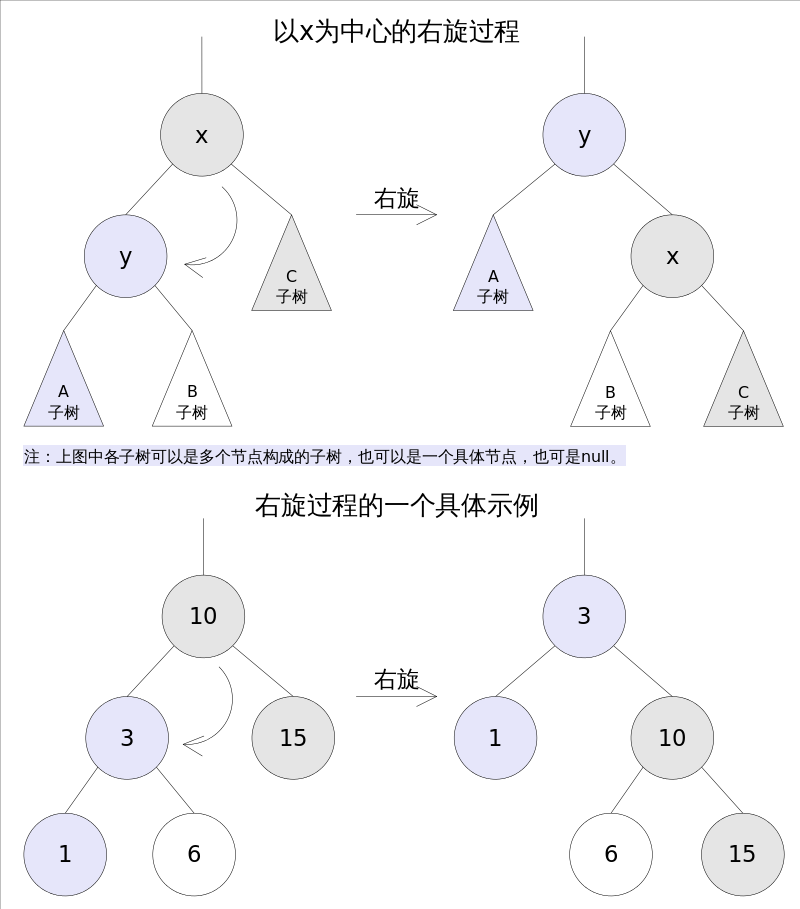
右旋是将X的左子树绕X顺时针旋转，使得X的左子树成为X的父亲，同时注意修改相关节点的引用，旋转之后要求仍然满足搜索树的属性

插入元素

红黑树5大特性

1. 每个节点要么是红色，要么是黑色。
2. 根节点是黑色。
3. 所有叶子节点（NIL）是黑色。
4. 如果一个节点是红色的，则它的两个子节点都是黑色的。
5. 对于每个节点，从该节点到其所有后代叶子节点的简单路径上，均包含相同数目的黑色节点。

红黑树的插入操作也需要保持红黑树的性质。插入操作的简单总结如下：

首先将红黑树当作一颗查找树一样将节点插入，然后将节点着为红色，最后通过旋转和重新着色的方法使之重新成为红黑树

1. 二叉搜索树插入：首先，像在普通的二叉搜索树中一样插入新节点。新插入的节点总是红色的。这是因为插入一个红色节点比插入一个黑色节点更不容易违反红黑树的性质。如果新插入的节点是根节点，那么在最后一步我们会改变它的颜色。

2. 调整：由于新插入的节点是红色的，因此可能会违反以下两个性质：

   • 性质2：根节点是黑色的（如果新插入的节点是根节点）。
   • 性质4：如果一个节点是红色的，则它的两个子节点都是黑色的（如果新插入的节点的父节点是红色的）。

现在我们来分析一下新增的节点（红色）插入之后可能面临的几种情况，以及他们的处理措施

1. 插入的节点为根节点
2. 新插入的节点的父亲节点为黑色
3. 新插入的节点的父亲节点为红色，叔叔节点（它的父节点的兄弟节点）为红色节点
4. 新插入的节点的父亲节点为红色，叔叔节点为黑色

1. 插入的节点是根节点

将新插入的红色节点变成黑色节点，满足根节点为黑色节点的要求！

2. 新插入的节点的父亲节点为黑色

这个时候不需要进行任何调整操作，此时的树仍然是一颗标准的红黑树

3. 新插入的节点的父亲节点为红色，叔叔节点（它的父节点的兄弟节点）为红色节点（不考虑左右）

解决方案：将叔叔和父亲节点改为黑色，爷爷节点改为红色，然后又将爷爷节点当作插入节点看待，一直进行上面的操作，直到当前节点为根节点，然后将根节点变成黑色，举例说明：

已有的一颗红黑树

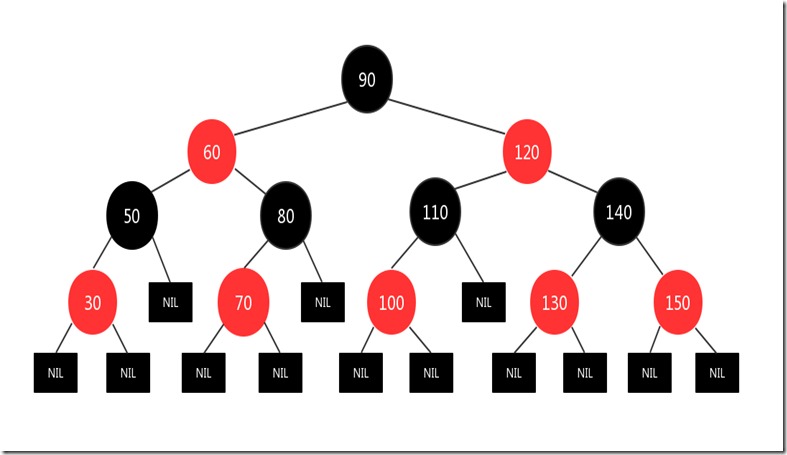
插入一个125的节点：

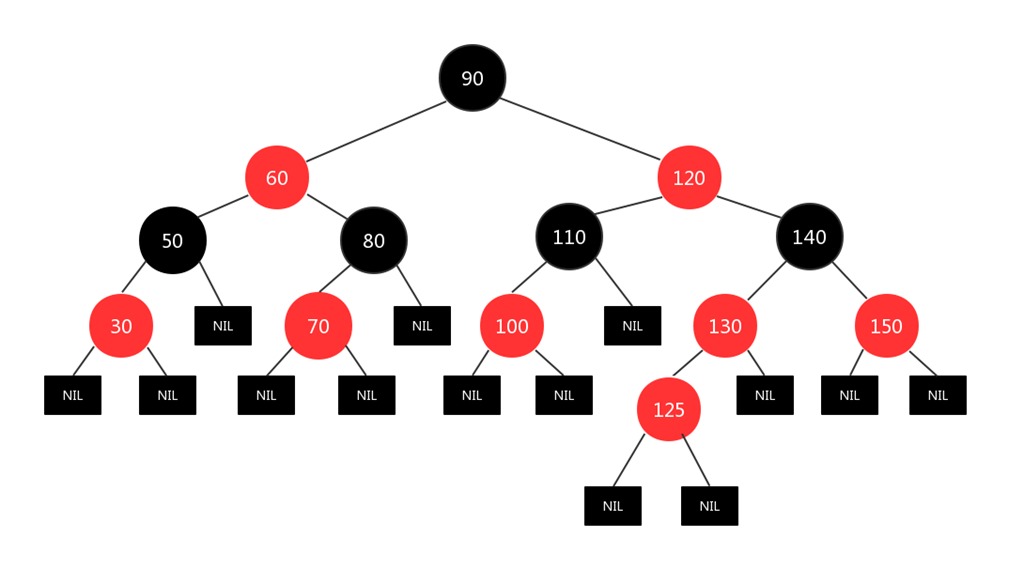
现在125节点和130节点都是红色的，显然违背了规则4，所以将新插入节点的父亲130节点和插入节点的叔叔节点150变成黑色，并将新插入节点的爷爷节点140变成红色，图如下：

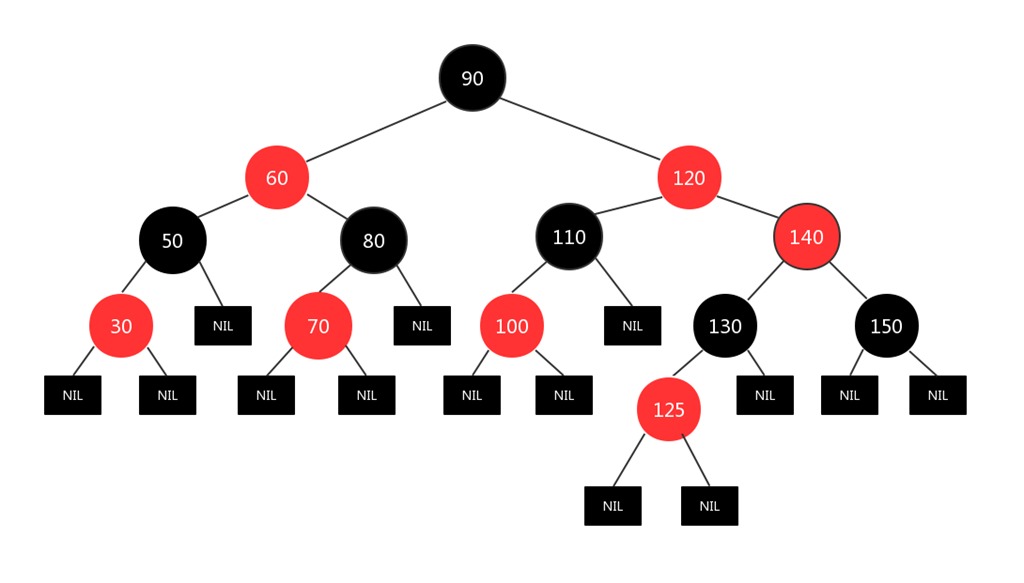
然后又将140节点当作新插入节点处理（因为140节点和新插入节点面临的情况都是一样的：和父亲节点都是红色），也就是做如下处理：将140节点的父亲节点120和140的叔叔节点60变成黑色节点，将140节点的爷爷节点变成红色，因为遍历到了根节点，要满足根节点是黑色的性质要求，所以又将140的爷爷节点也就是根节点变成黑色，图如下：

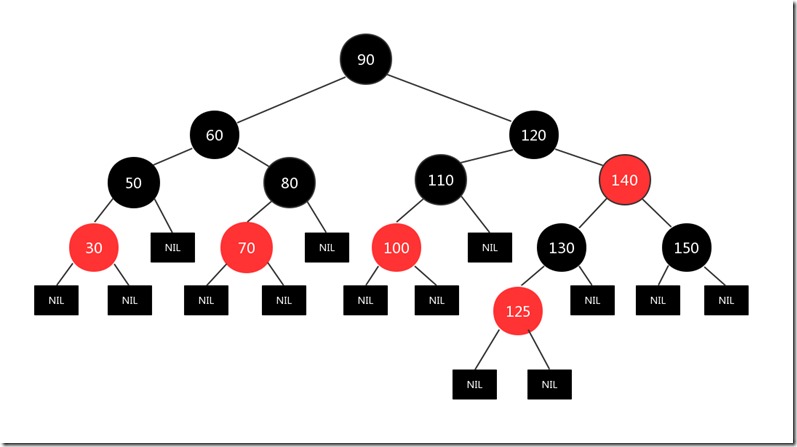
到这里，为新插入节点125所做的某些节点重新着色的操作就完成了，现在该树是标准的红黑树了！

4. 新插入的节点的父亲节点为红色，叔叔节点为黑色

4.1. 父亲节点为爷爷节点的左孩子，新插入节点为父节点的左孩子（左左情况）

4.2 父亲节点为爷爷节点的右孩子，新插入节点为父亲节点的右孩子（右右情况）

4.3 父亲节点为爷爷节点的左孩子，新插入节点为父节点的右孩子（左右情况）

4.4 父亲节点为爷爷节点的左孩子，新插入节点为父节点的左孩子（右左情况）

这4种情况中，4.1 和 4.2 的处理方法是一样的，4.3和4.4的处理方法是也是一样的，现在分开说明下。

左左和右右的情况下举例说明：

比如下图，新插入节点为25，其父亲节点30为红色，其叔叔节点为空黑色叶子节点，且新插入节点和其父节点都是左孩子：

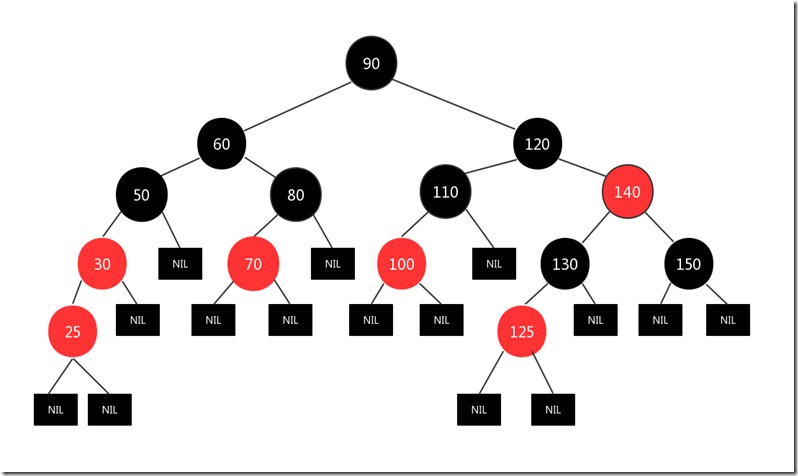
我们将其父亲节点和爷爷节点颜色互换，然后针对爷爷节点进行一次左旋，图如下：

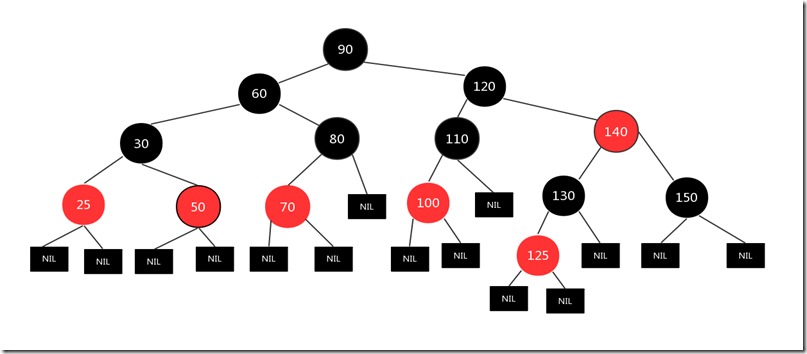
现在这颗树完全满足红黑树的5个性质了（最好自己对照5个性质看一下）

现在又一个问题，我们为什么要进行旋转？

假设我们只将新增节点的父亲节点和其爷爷节点的颜色互换了，图如下：

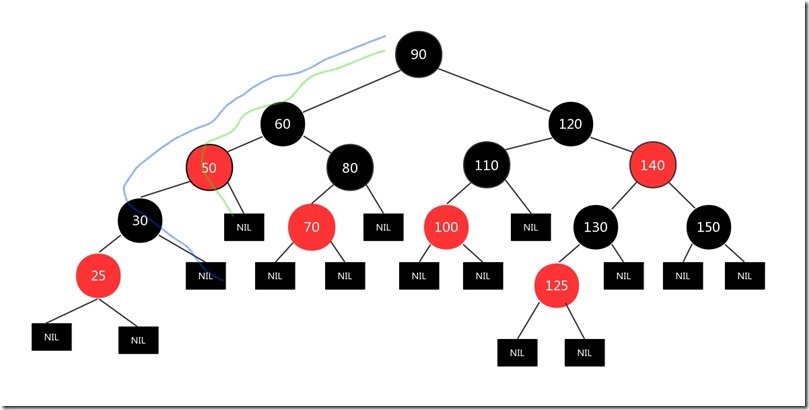
我们发现上述两条到叶子节点的路径经过的黑色节点数量不一样！！！，所以它不满足红黑树的第5条性质，所以这就是我们旋转的意义所在！！！（因为无论你怎么旋转都没有改变节点颜色，改变的是节点的位置，而这位置改变刚好能使得树满足红黑树的第5条性质！）

左右和右左的情况举例说明

比如下图，新插入节点是126，其父节点125为红色，其叔叔节点为空的黑色节点，而且插入节点是右节点，父节点是左节点

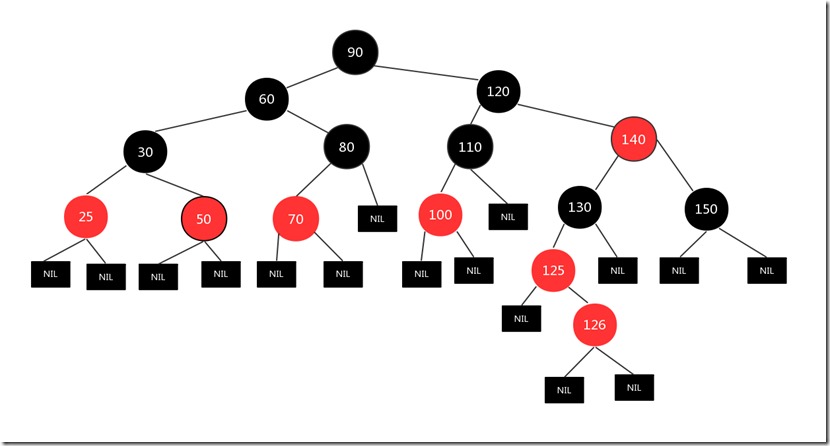
我们将父亲节点125看作当前节点进行左旋，旋转结果如下：

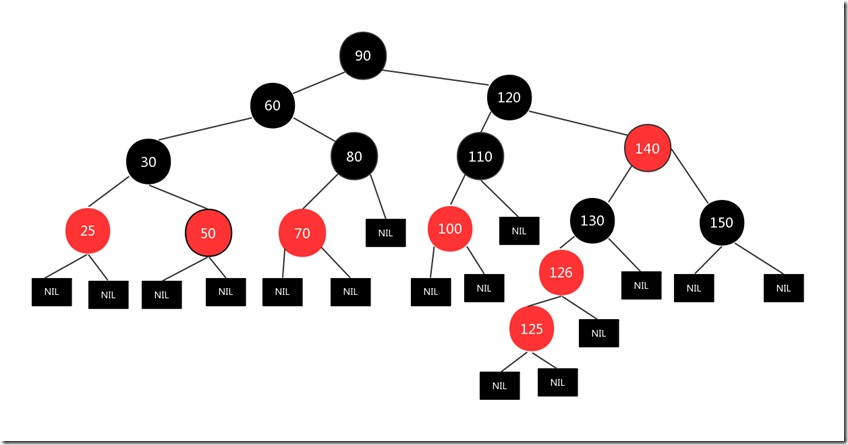
现在我们的当前节点是125，现在125的处境和上面的情况4是一样的（父节点为红，叔叔节点为黑，插入节点为左节点，父亲节点也为左孩子）现在我们继续按照情况4的处理办法处理上述情况（措施和情况4一样，父亲节点和爷爷节点互换颜色，然后针对爷爷节点进行左旋），处理后情况如下：

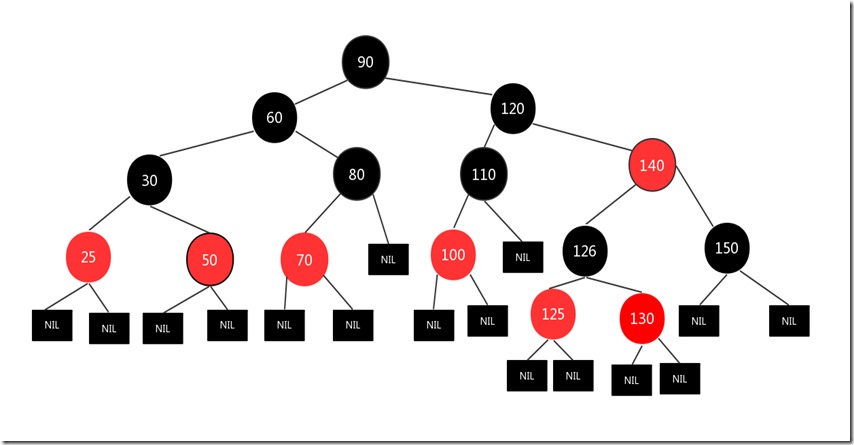
现在树就是一颗标准的红黑树了！

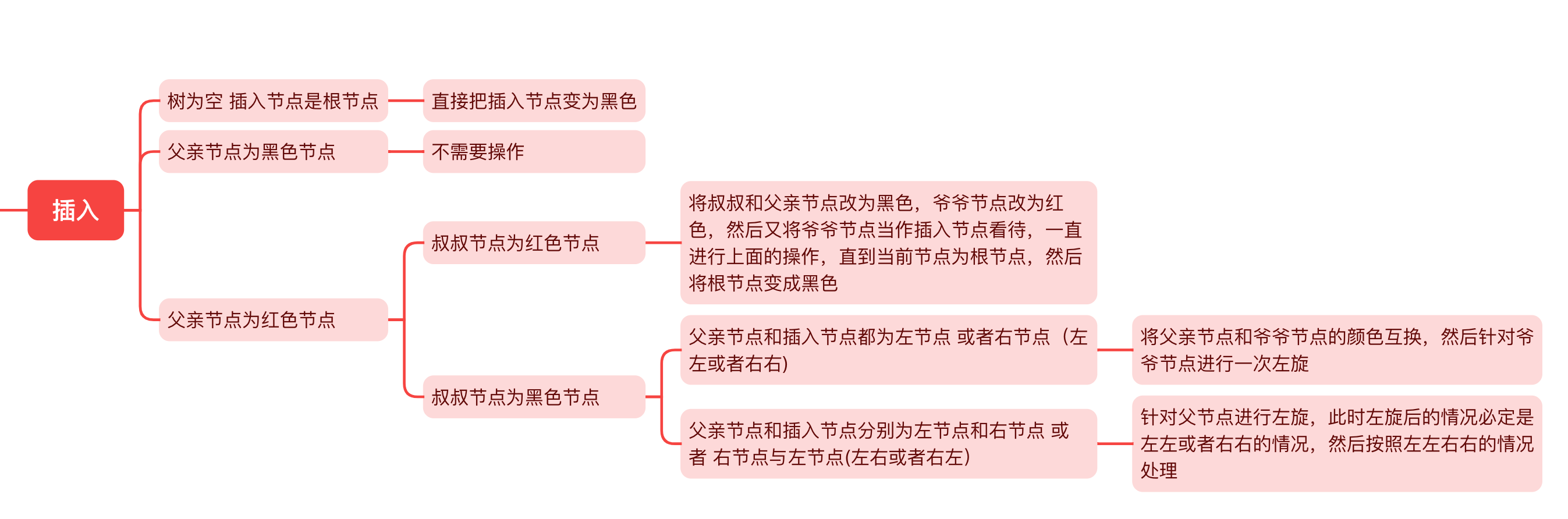
插入总结

我们现在总结一下插入节点面临的几种情况以及采取的措施：

删除元素

先说删除节点的过程原理：首先将红黑树当作一个二叉查找树，将该节点从二叉查找树种删除，然后通过一些列重新着色操作等一系列措施来修正该树，使之重新成为一颗红黑树，删除节点其实很容易，难的是如何使得删除节点后的树重新成为一个红黑树

我们可以根据删除节点的儿子个数分为三种情况：

1. 删除节点没有儿子
2. 删除节点有1个儿子
3. 删除节点有2个儿子

下面我们对这三种情况继续细分

1. 删除的节点没有儿子

1.1 删除节点为红色

1.2 删除节点为黑色，其兄弟节点没有儿子

1.3 删除节点为黑色，其兄弟节点有一个孩子不空，并且该孩子和兄弟节点在同一边（同时为左子树或者右子树）

1.4 删除节点为黑色，其兄弟节点有一个孩子不空，并且该孩子和兄弟节点不在同一边（分别为左右子树或者右左子树）

1.5 删除节点为黑色，其兄弟节点有两个孩子，而且兄弟节点为黑色

1.6 删除节点为黑色，其兄弟节点有两个孩子，而且兄弟节点为红色

1.1 删除节点为红色

直接删除，比如下图，想要删除130节点

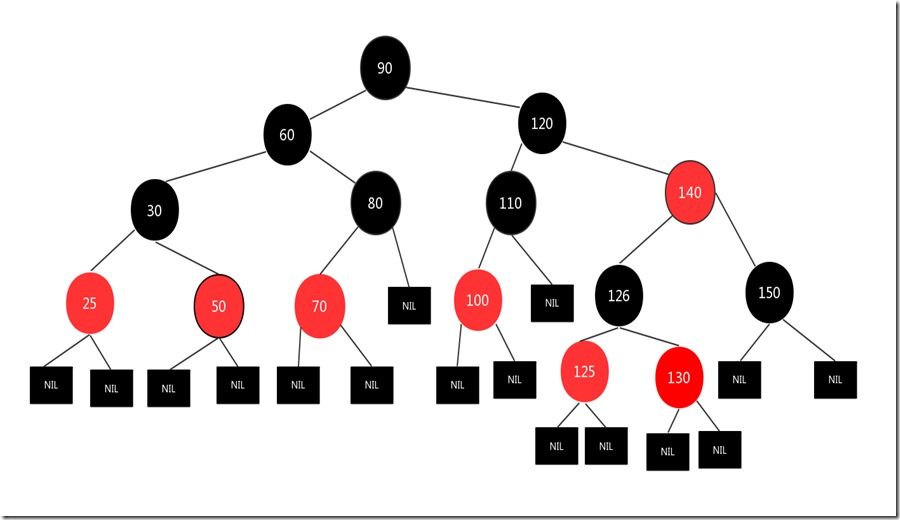
直接删除130节点，结果图如下：

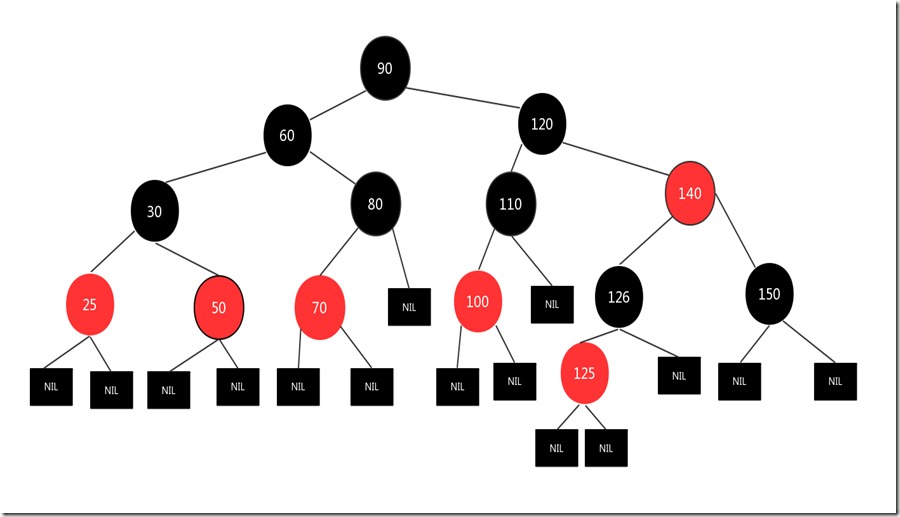
因为删除的是红色节点，不会影响红黑树第5条性质，所以可以直接删除

1.2 删除节点为黑色，其兄弟节点没有儿子

这种情况下其兄弟节点也肯定是黑色的（要满足红黑树第5条性质），假设现在要删除的是150这个节点，原图如下

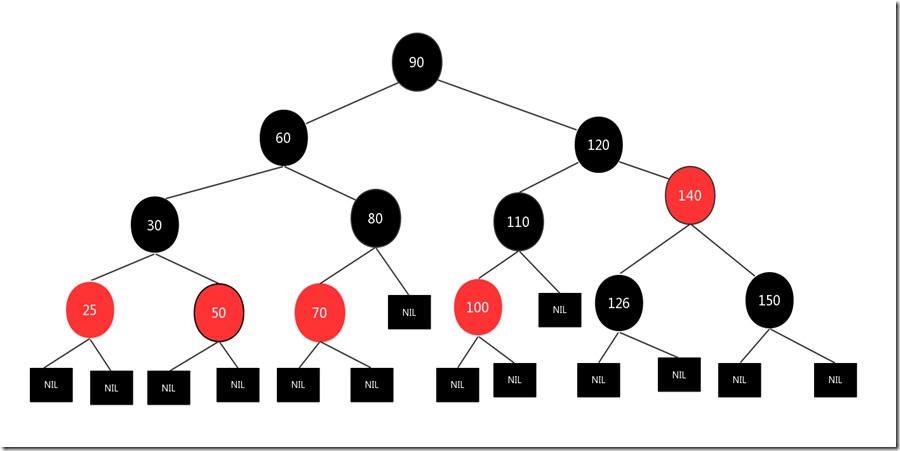
先删除节点150，然后将兄弟节点126变成红色，父亲节点140变成黑色，结果如下：

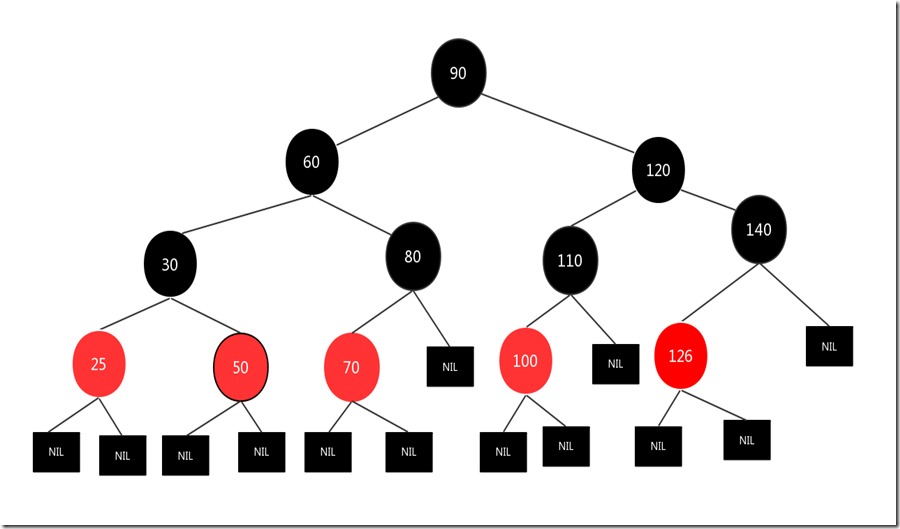
这样做的目的是为了满足红黑树的第5条性质，要不然根到最右边的叶子节点经过的黑色节点只有3个，而其他路径有4个

1.3 删除节点为黑色，其兄弟节点有一个孩子不空，并且该孩子和兄弟节点在同一边（同时为左子树或者右子树）

假设现在要删除的节点为110，其兄弟节点140只有一个孩子150，而且都是右子树，满足上述条件，原图如下：

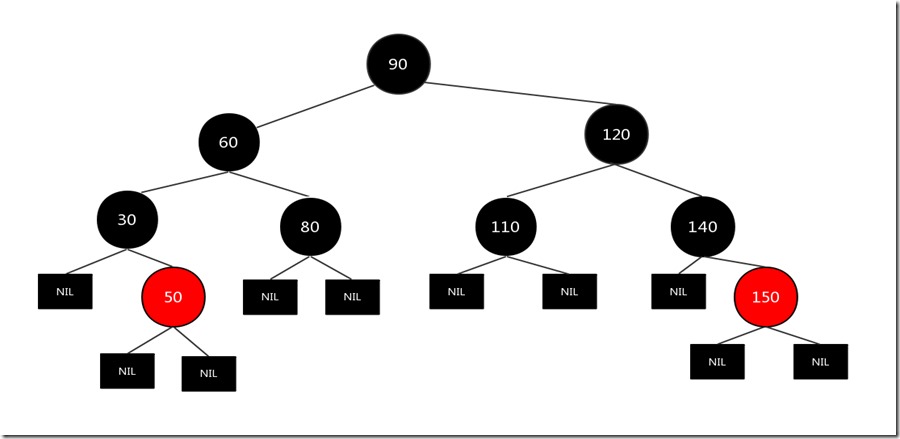
先把需要删除的节点110删除，然后这个时候需要交换兄弟节点140和父亲节点120的颜色，并且把父亲节点120涂成黑色，把兄弟节点的子节点150涂成黑色

1.3.1 如果兄弟节点和兄弟节点的儿子都在右子树的话：对父亲节点进行左旋

1.3.2 如果兄弟节点和兄弟节点的儿子都在左子树的话：对父亲节点进行右旋

上图是第一种情况，所以对父节点120进行左旋，结果如下：

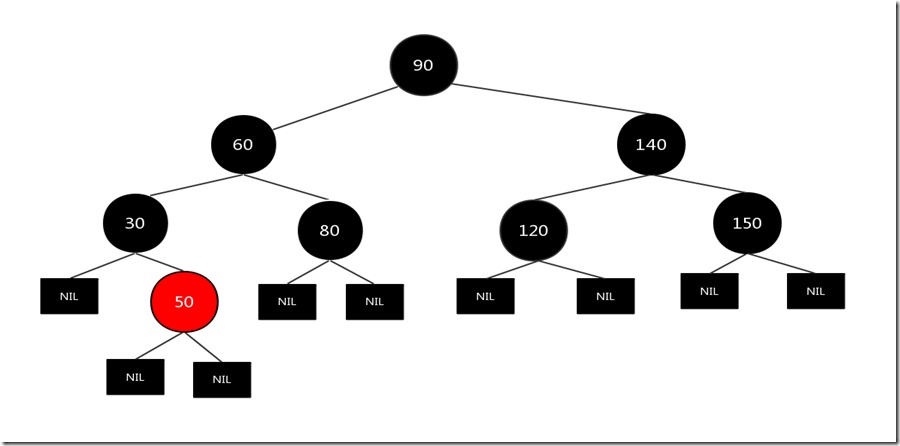
通过对某些节点重新着色和旋转，又将该树变成了一个标准的红黑树了

1.4 删除节点为黑色，其兄弟节点有一个孩子不空，并且该孩子和兄弟节点不在同一边（分别为左右子树或者右左子树）

这种情况下，兄弟节点的儿子50节点只能为红色，要不然满足不了红黑树的第5条性质

假设我们现在要删除的节点是80节点，其兄弟节点只有一个儿子，而且兄弟节点和兄弟节点的儿子是左右的情况（兄弟节点为左节点，兄弟节点的儿子为右节点），符合上述要求，原图如下

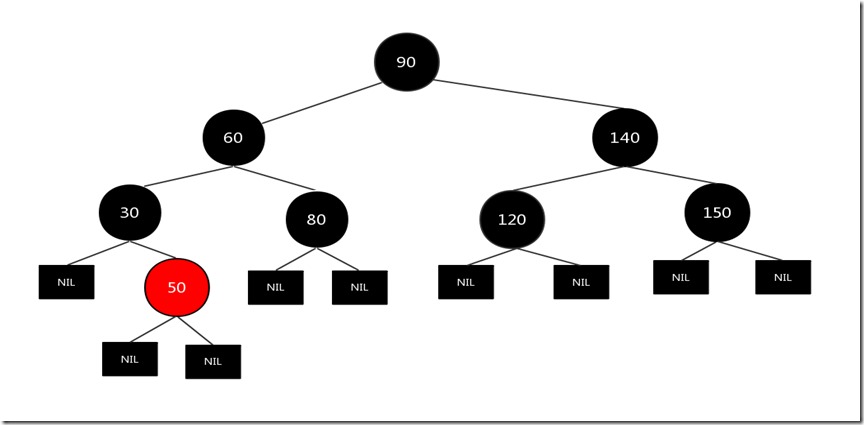
现在我们先将需要删除的80节点删除，然后将兄弟节点和兄弟节点的儿子节点颜色互换

1.4.1 如果兄弟节点是左子树，兄弟节点的儿子节点是右子树：对兄弟节点进行左旋

1.4.2 如果兄弟节点是右子树，兄弟节点的儿子节点是左子树：对兄弟节点进行右旋

上图的情况是1.4.1 进行左旋，也就是对兄弟节点30进行左旋，结果如下图：

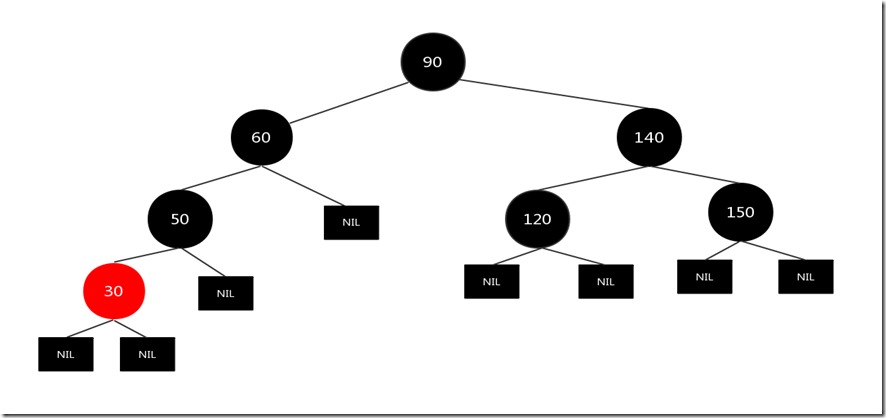
注意！！，现在还没有结束变换，我们发现变换之后的红黑树情况和情况3中的情况很相似，兄弟节点50和兄弟节点的子节点30处在同一边，我们可以按照情况3的处理办法进行处理：

交换兄弟节点50和父亲节点60的颜色，把父亲节点60和兄弟节点的子节点30涂成黑色

1.4.3 如果兄弟节点和兄弟节点的儿子都在右子树的话：对父亲节点进行左旋

1.4.4 如果兄弟节点和兄弟节点的儿子都在左子树的话，对父亲节点进行右旋

上图的情况是1.4.4 对父亲节点60进行右旋，结果如下：

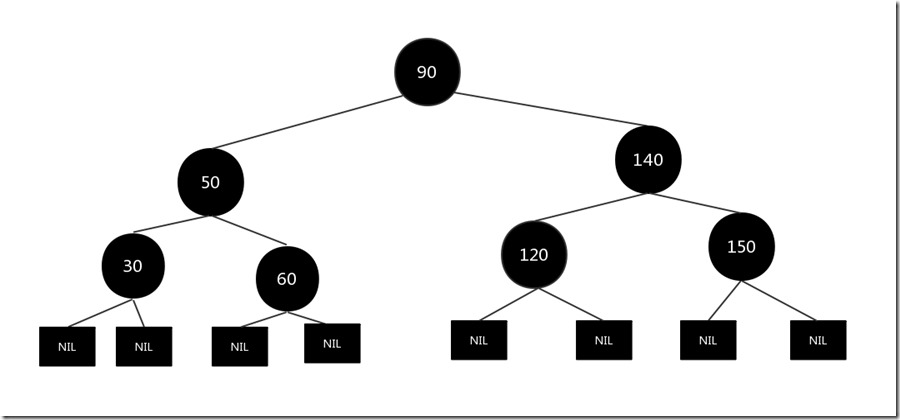
通过对某些节点重新着色和旋转，又将该树变成了一个标准的红黑树了

1.5 删除节点为黑色，其兄弟节点有两个孩子，而且兄弟节点为黑色

现在我们假设要删除的节点是130节点，其兄弟节点有两个孩子（可以把空的叶子节点看成黑色的儿子节点），而且兄弟节点和兄弟节点的儿子节点都是黑色，符合上述情况，原图如下：

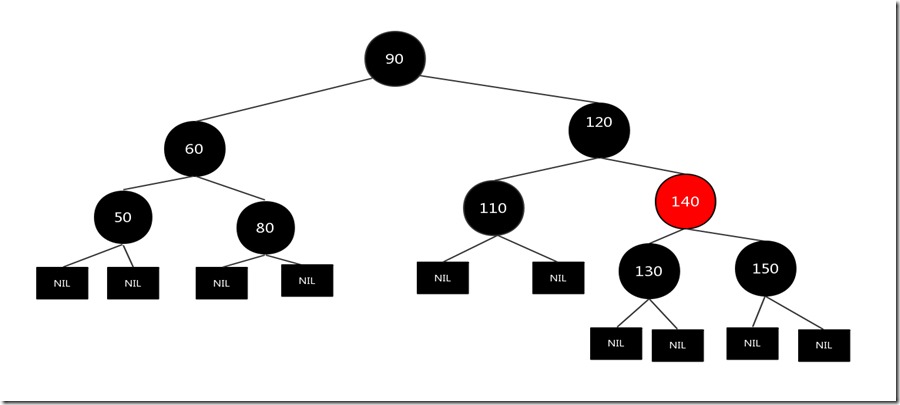
先直接删除需要删除的节点130，然后将父亲节点140和兄弟节点150颜色互换即可，结果如下：

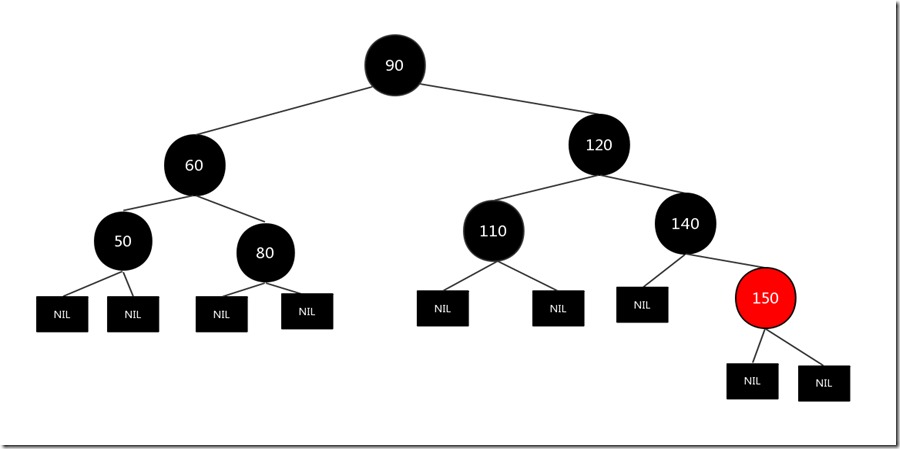
1.6 删除节点为黑色，其兄弟节点有两个孩子，而且兄弟节点为红色

假设我们要删除的节点是110，其兄弟节点140为红色而且有两个孩子，原图如下：

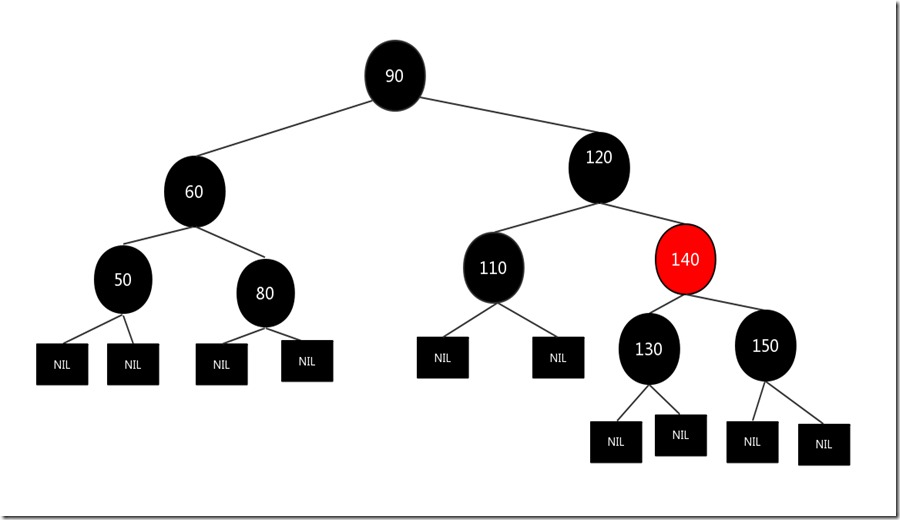
我们先交换兄弟节点140和父亲节点120的颜色

1.6.1 被删除的元素为左子树：对父亲节点左旋

1.6.2 被删除的元素为右子树：对父亲节点右旋

上图的情况是1.6.1的情况，所以我们对父亲节点140进行左旋，按照上面操作之后（未完），结果如下：

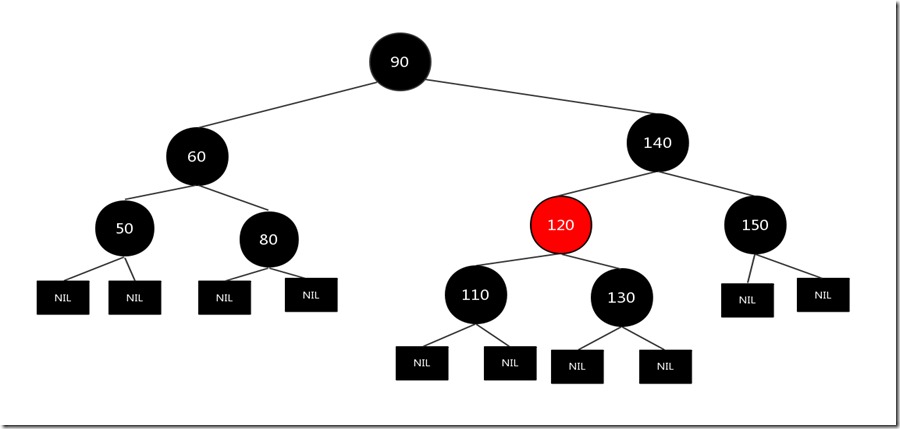
我们发现完成上述操作之后树还不是一个标准的红黑树（到叶子节点的一条路径黑色节点只有3个，而其他的路径有4个），我们发现现在红黑树的情况又和情况1.5的很像，所以我们按照情况1.5的做法继续：

我们要需要删除的节点还没有被删除（我特意留到最后删除的，就是为了在这里表示父亲节点是谁的父亲节点...）,现在我们将父亲节点120和兄弟节点130的颜色互换即可，结果如下：

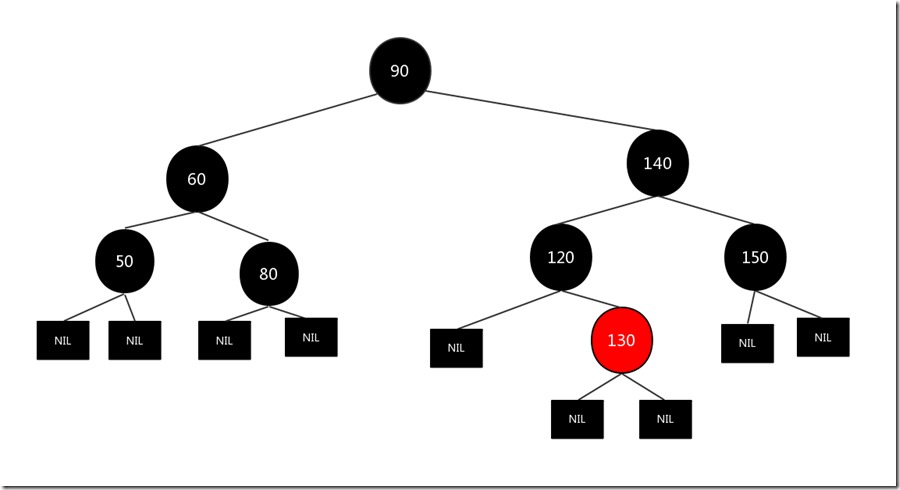
现在该树变成了一个标准的红黑树了

2. 删除节点仅有一个儿子节点

2.1 删除节点为黑色，儿子节点无论左右都可以

2.2 删除节点为红色

下面我们来分情况讨论

2.1 删除节点为黑色，儿子节点无论左右都可以

比如我们要删除的节点是120节点，删除节点为黑色，唯一的儿子节点130为红色（必须是红色，不然违背红黑树第5条性质）原图如下：

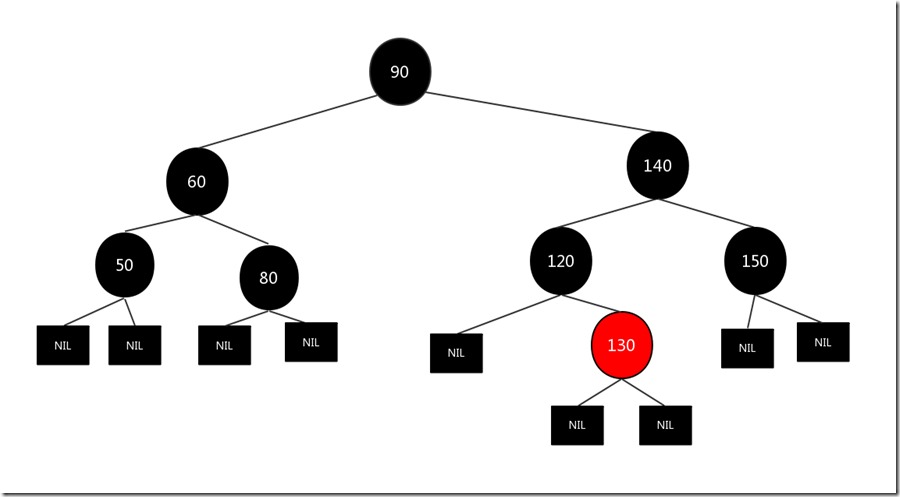
我们将需要删除的节点120删除，然后将子节点130涂黑放到被删除节点120的位置，结果如下：

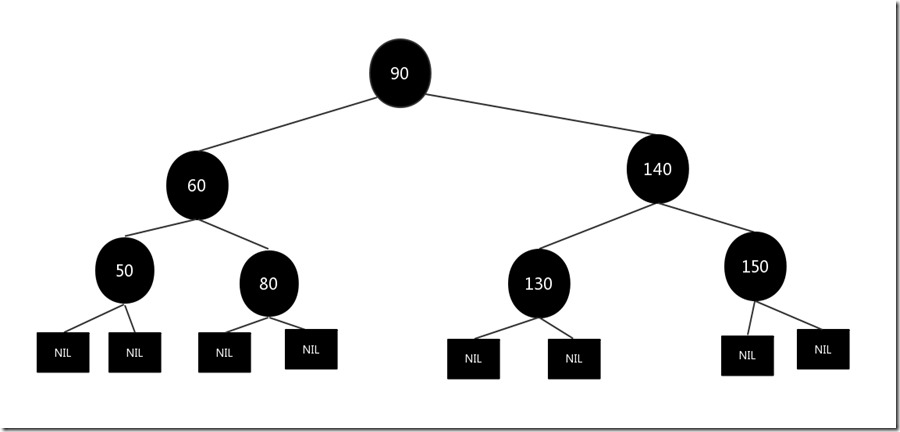
2.2 删除节点为红色

其儿子节点只能为黑，红黑树中不存在这种情况，要不然无法满足红黑树第5条性质

3. 删除节点有两个儿子节点

找到删除节点的右子树中最左的节点，两两值交换，然后删除节点的情况就变成了上面两种情况中的一种了

3.1 删除节点只有一个儿子的情况

3.2 删除节点没有儿子的情况

假设要删除的节点是120，图如下：

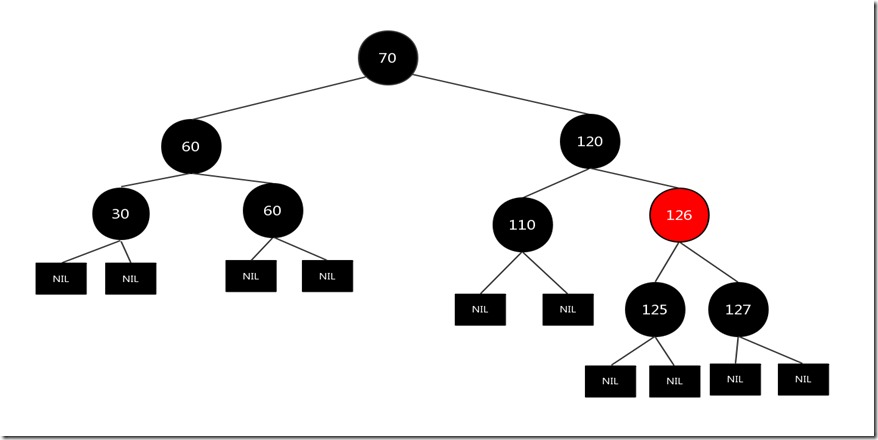
先找到节点120右子树中最左的节点125，交换两者的值

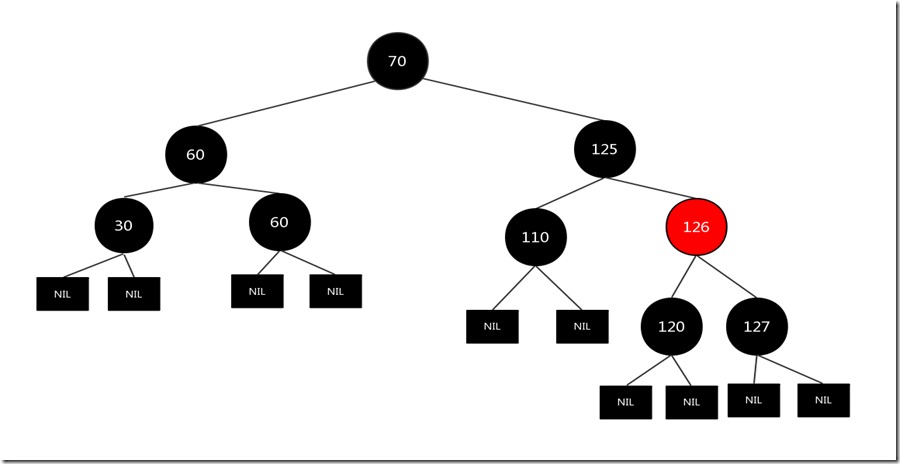
现在120仍然是要删除的节点，我们发现删除节点120没有一个儿子，而且其兄弟节点也没有儿子，那么其对应的情况为：

1.2的情况：删除节点为黑色，其兄弟节点没有儿子

按照1.2 的处理逻辑以后，变为

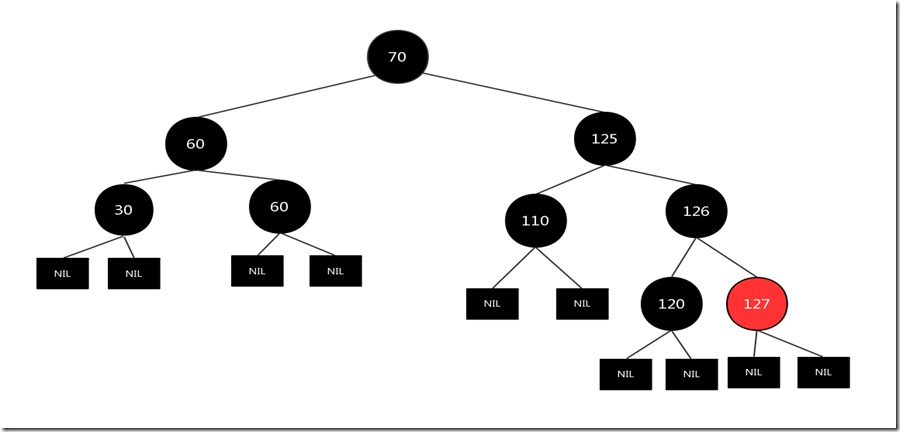
现在该树变成了一个标准的红黑树了

所以当删除节点右两个儿子节点的时候，我们只需要按照搜索二叉树的删除方法替换删除值，这样就可以将情况变成删除节点没有儿子节点或者1个儿子节点的情况处理了。

删除总结

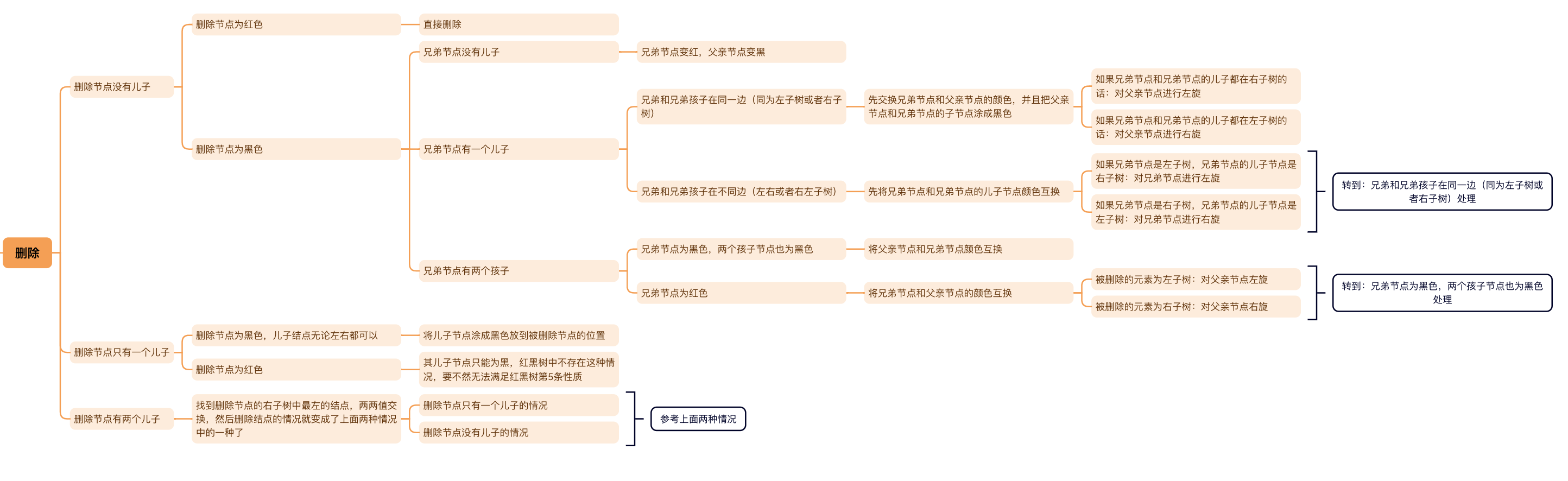
红黑树极简总结

五大特性

红黑树是一种自平衡二叉搜索树，它在插入和删除操作中保持了大致的平衡，从而保证了搜索操作的效率。在学习红黑树时，应当关注以下重要特性（红黑树五大特性）：

1. 节点颜色：每个节点都被涂上红色或黑色。
2. 根节点性质：树的根节点总是黑色的。
3. 红色节点性质：如果一个节点是红色的，则它的子节点必须是黑色的（也就是说，红色节点不能有红色的子节点，即不允许出现连续的红色节点）。
4. 每个叶子节点（NIL节点）是黑色的：这里的叶子节点是指树尾端的空（null）叶子节点。
5. 黑色高度性质：从任一节点到其每个叶子节点的所有路径都包含相同数目的黑色节点。

常见操作

红黑树的添加删除：当通过插入或删除操作改变了树结构时，可能需要通过一系列的旋转和重新着色来恢复红黑树的特性。

时间复杂度

这些特性共同保证了红黑树的一个关键性质：从根到叶子的最长路径不会超过最短路径的两倍长度。因此，在最坏的情况下，查找操作的时间复杂度保持在 O(logn)，其中 n 是树中元素的数量。

在实际应用中，Java的TreeMap和TreeSet是基于红黑树实现的。

红黑树的插入和删除操作的时间复杂度也是 O(logn)，其中 n 是树中元素的数量。

• 插入操作：首先需要进行一次标准的二叉搜索树插入，时间复杂度为 O(logn)。然后可能需要进行一系列的颜色变更和树旋转来维护红黑树的性质。尽管可能需要多次旋转，但旋转操作的数量是有上限的，因此插入操作的总体时间复杂度仍然是 O(logn)。
• 删除操作：删除操作首先进行一次标准的二叉搜索树删除，时间复杂度为 O(logn)。如果被删除的节点是红色的，通常不会破坏红黑树的性质。如果被删除的节点是黑色的，可能需要进行额外的操作来重新平衡树，这包括重新着色和旋转。和插入一样，这些操作的数量也是有限的，因此删除操作的时间复杂度也是 O*(logn)。

使用场景

由于红黑树是平衡的，所以树的高度始终保持在 O(logn)，这保证了所有的搜索、插入和删除操作都可以在对数时间内完成，这是红黑树的一个关键优点，尤其在需要快速查找的同时也需要快速插入和删除的场景中非常有用。

TreeMap源码解析

铺垫了那么多，终于可以来深入TreeMap的源码了。

构造函数

//比较器
private final Comparator<? super K> comparator;

//根节点
private transient Entry<K,V> root;

static final class Entry<K,V> implements Map.Entry<K,V> {
  			//节点key
        K key;
  			//节点value
        V value;
  			//左子节点
        Entry<K,V> left;
  			//右子节点
        Entry<K,V> right;
  			//父节点
        Entry<K,V> parent;
  			//是红色节点还是黑色节点
        boolean color = BLACK;
}

public TreeMap() {
    comparator = null;
}

//指定比较器
public TreeMap(Comparator<? super K> comparator) {
    this.comparator = comparator;
}

//传入已有的map
public TreeMap(Map<? extends K, ? extends V> m) {
    comparator = null;
    putAll(m);
}

//传入已经排序好的map
public TreeMap(SortedMap<K, ? extends V> m) {
    comparator = m.comparator();
    try {
        buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
    } catch (java.io.IOException cannotHappen) {
    } catch (ClassNotFoundException cannotHappen) {
    }
}

构造函数比较简单，没啥好说的

get()

public V get(Object key) {
    // 调用getEntry方法
    Entry<K,V> p = getEntry(key);
    return (p==null ? null : p.value);
}

final Entry<K,V> getEntry(Object key) {
    // 如果比较器不为空 则使用比较器查找
    if (comparator != null)
        return getEntryUsingComparator(key);
    // 禁止null 的 key
    if (key == null)
        throw new NullPointerException();
    @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
    // 从根节点开始
    Entry<K,V> p = root;
    // 遍历树直到叶子节点
    while (p != null) {
        // 比较键和当前节点键的大小
        int cmp = k.compareTo(p.key);
        // 如果小于当前节点键，则向左子树遍历
        if (cmp < 0)
            p = p.left;
        // 如果大于当前节点键，则向右子树遍历
        else if (cmp > 0)
            p = p.right;
        // 找到了键对应的节点，返回该节点
        else
            return p;
    }
    // 没有找到键对应的节点，返回null
    return null;
}


final Entry<K,V> getEntryUsingComparator(Object key) {
    @SuppressWarnings("unchecked")
        K k = (K) key;
    // 获取比较器
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        // 从根节点开始
        Entry<K,V> p = root;
        // 遍历树直到叶子节点
        while (p != null) {
            // 使用比较器比较键和当前节点键的大小
            int cmp = cpr.compare(k, p.key);
            // 如果小于当前节点键，则向左子树遍历
            if (cmp < 0)
                p = p.left;
            // 如果大于当前节点键，则向右子树遍历
            else if (cmp > 0)
                p = p.right;
            // 找到了键对应的节点，返回该节点
            else
                return p;
        }
    }
    // 没有找到键对应的节点，返回null
    return null;
}

get() 方法比较好理解，整个流程如图

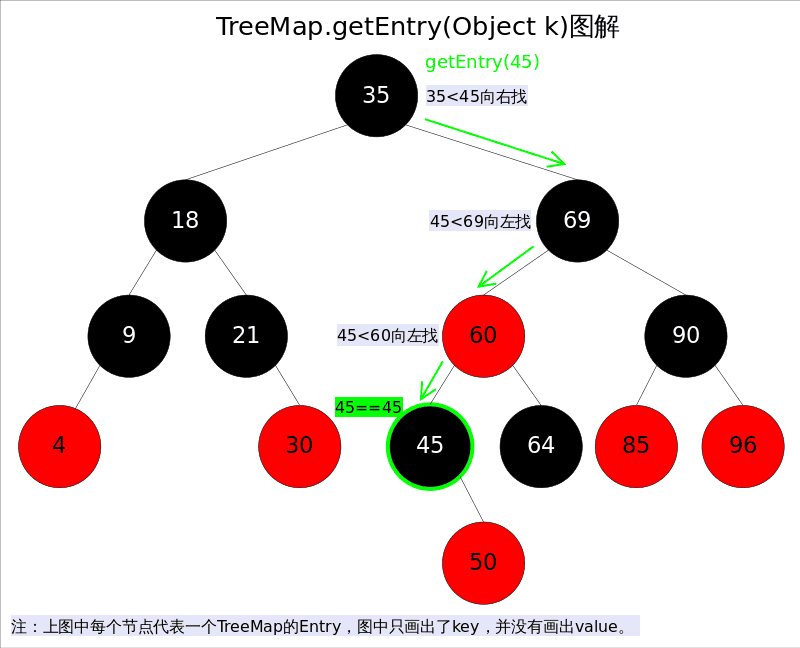
put()

put()方法外部的逻辑也是简单的，比较困难的点在于，新增一个节点后如何调整才能继续满足红黑树的性质，也就是方法fixAfterInsertion()

// 定义一个公共方法用于将指定的键值对放入到树中
public V put(K key, V value) {
    // 从根节点开始
    Entry<K,V> t = root;
    // 如果根节点为空，即树为空
    if (t == null) {
        // 比较键自身
        compare(key, key); 

        // 创建新的节点作为根节点
        root = new Entry<>(key, value, null);
        // 树的大小设置为1
        size = 1;
        // 修改次数加1
        modCount++;
        // 由于之前树为空，现在已添加节点，返回null
        return null;
    }
    // 定义比较结果变量
    int cmp;
    // 定义父节点
    Entry<K,V> parent;

    //比较器
    Comparator<? super K> cpr = comparator;
    if (cpr != null) {
        // 循环直到找到合适的插入位置
        do {
            // 设置当前节点为父节点
            parent = t;
            // 使用比较器比较键
            cmp = cpr.compare(key, t.key);
            // 如果键小于当前节点的键，向左子树遍历
            if (cmp < 0)
                t = t.left;
            // 如果键大于当前节点的键，向右子树遍历
            else if (cmp > 0)
                t = t.right;
            // 如果键等于当前节点的键，更新当前节点的值
            else
                return t.setValue(value);
        } while (t != null);
    }
    else {
        // 如果键为null，则抛出空指针异常
        if (key == null)
            throw new NullPointerException();
        // 忽略类型检查警告（假设键是可比较的）
        @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
        // 循环直到找到合适的插入位置
        do {
            // 设置当前节点为父节点
            parent = t;
            // 使用键的自然顺序比较键
            cmp = k.compareTo(t.key);
            // 如果键小于当前节点的键，向左子树遍历
            if (cmp < 0)
                t = t.left;
            // 如果键大于当前节点的键，向右子树遍历
            else if (cmp > 0)
                t = t.right;
            // 如果键等于当前节点的键，更新当前节点的值
            else
                return t.setValue(value);
        } while (t != null);
    }
    // 创建新的节点
    Entry<K,V> e = new Entry<>(key, value, parent);
    // 如果比较结果小于0，新节点成为父节点的左子节点
    if (cmp < 0)
        parent.left = e;
    // 否则，新节点成为父节点的右子节点
    else
        parent.right = e;
    // 插入新节点后修复红黑树的性质（调整）
    fixAfterInsertion(e);
    // 树的大小加1
    size++;
    // 修改次数加1
    modCount++;
    // 插入新节点，返回null
    return null;
}

可以看到 put的寻找节点的逻辑跟get寻找节点的逻辑基本一样，核心变化在与 插入节点以后需要自平衡（调整），我们来看下自平衡的代码fixAfterInsertion

// 修复插入操作后的红黑树属性
private void fixAfterInsertion(Entry<K,V> x) {
    // 新插入的节点颜色设为红色
    x.color = RED;

    // 当x不是根节点且x的父节点为红色时循环处理
    while (x != null && x != root && x.parent.color == RED) {
        // 如果x的父节点是其爷爷节点的左子节点
        if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
            // 获取x的叔叔节点y
            Entry<K,V> y = rightOf(parentOf(parentOf(x)));
            // 如果叔叔节点y是红色
            if (colorOf(y) == RED) {
                // 将x的父节点设为黑色
                setColor(parentOf(x), BLACK);
                // 将叔叔节点设为黑色
                setColor(y, BLACK);
                // 将x的爷爷节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                // 将x指向其爷爷节点，继续循环判断
                x = parentOf(parentOf(x));
            } else {
                // 如果x是其父节点的右子节点
                if (x == rightOf(parentOf(x))) {
                    // 将x指向其父节点
                    x = parentOf(x);
                    // 对x进行左旋
                    rotateLeft(x);
                }
                // 将x的父节点设为黑色
                setColor(parentOf(x), BLACK);
                // 将x的爷爷节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                // 对x的爷爷节点进行右旋
                rotateRight(parentOf(parentOf(x)));
            }
        } else {
            // 如果x的父节点是其爷爷节点的右子节点
            Entry<K,V> y = leftOf(parentOf(parentOf(x)));
            // 如果叔叔节点y是红色
            if (colorOf(y) == RED) {
                // 将x的父节点设为黑色
                setColor(parentOf(x), BLACK);
                // 将叔叔节点设为黑色
                setColor(y, BLACK);
                // 将x的爷爷节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                // 将x指向其爷爷节点，继续循环判断
                x = parentOf(parentOf(x));
            } else {
                // 如果x是其父节点的左子节点
                if (x == leftOf(parentOf(x))) {
                    // 将x指向其父节点
                    x = parentOf(x);
                    // 对x进行右旋
                    rotateRight(x);
                }
                // 将x的父节点设为黑色
                setColor(parentOf(x), BLACK);
                // 将x的爷爷节点设为红色
                setColor(parentOf(parentOf(x)), RED);
                // 对x的爷爷节点进行左旋
                rotateLeft(parentOf(parentOf(x)));
            }
        }
    }
    // 设置根节点为黑色
    root.color = BLACK;
}



// 获取节点p的颜色
private static <K,V> boolean colorOf(Entry<K,V> p) {
    return (p == null ? BLACK : p.color);
}

// 获取节点p的父节点
private static <K,V> Entry<K,V> parentOf(Entry<K,V> p) {
    return (p == null ? null: p.parent);
}

// 设置节点p的颜色
private static <K,V> void setColor(Entry<K,V> p, boolean c) {
    if (p != null)
        p.color = c;
}

// 获取节点p的左子节点
private static <K,V> Entry<K,V> leftOf(Entry<K,V> p) {
    return (p == null) ? null: p.left;
}

// 获取节点p的右子节点
private static <K,V> Entry<K,V> rightOf(Entry<K,V> p) {
    return (p == null) ? null: p.right;
}

// 对节点p进行左旋转
private void rotateLeft(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> r = p.right; // 获取p的右子节点r
        p.right = r.left; // 将r的左子节点设置为p的右子节点
        if (r.left != null)
            r.left.parent = p; // 如果r的左子节点不为空，设置其父节点为p
        r.parent = p.parent; // 将r的父节点设置为p的父节点

        // 如果p的父节点为空，将r设置为根节点
        if (p.parent == null)
            root = r;
        // 如果p是其父节点的左子节点，将r设置为p父节点的左子节点
        else if (p.parent.left == p)
            p.parent.left = r;
        else // 否则，将r设置为p父节点的右子节点
            p.parent.right = r;

        r.left = p; // 将p设置为r的左子节点
        p.parent = r; // 将p的父节点设置为r
    }
}

// 对节点p进行右旋转
private void rotateRight(Entry<K,V> p) {
    if (p != null) {
        Entry<K,V> l = p.left; // 获取p的左子节点l
        p.left = l.right; // 将l的右子节点设置为p的左子节点
        if (l.right != null) l.right.parent = p; // 如果l的右子节点不为空，设置其父节点为p
        l.parent = p.parent; // 将l的父节点设置为p的父节点

        // 如果p的父节点为空，将l设置为根节点
        if (p.parent == null)
            root = l;
        // 如果p是其父节点的右子节点，将l设置为p父节点的右子节点
        else if (p.parent.right == p)
            p.parent.right = l;
        else // 否则，将l设置为p父节点的左子节点
            p.parent.left = l;

        l.right = p; // 将p设置为l的右子节点
        p.parent = l; // 将p的父节点设置为l
    }
}

这里我添加了详细的注释，可以对着上面写的红黑树插入逻辑遇到的各种情况，可以清楚的看到代码是如何处理每种情况。

remove

remove方法的逻辑对应的就是上面红黑树删除元素的处理逻辑，具体代码我添加了详细的注释

// 删除键为key的节点，并返回其对应的值
public V remove(Object key) {
  	//先找到对应key的节点
    Entry<K,V> p = getEntry(key); 
    if (p == null) // 如果节点不存在，返回null
        return null;

    V oldValue = p.value; // 保存节点的旧值
    deleteEntry(p); // 删除节点
    return oldValue; // 返回旧值
}

// 删除节点p，并修复红黑树
private void deleteEntry(Entry<K,V> p) {
    modCount++; // 增加修改次数
    size--; // 减少树的大小

    // 如果p有两个子节点，找到p的后继节点s，将s的键值复制到p，然后将p指向s
    if (p.left != null && p.right != null) {
        Entry<K,V> s = successor(p);
        p.key = s.key;
        p.value = s.value;
        p = s;
    }

  	//这里看代码需要注意，p是需要删除的节点！！
    //replacement 是p的某一个子节点，最终要取代p节点的节点
    Entry<K,V> replacement = (p.left != null ? p.left : p.right);

   //p只有一棵子树非空。
    if (replacement != null) {
        // 将replacement指向p的父节点
        replacement.parent = p.parent;
        if (p.parent == null) // 如果p是根节点，replacement成为新的根
            root = replacement;
        else if (p == p.parent.left) // 如果p是左子节点，将设为其父节点的左子节点
            p.parent.left  = replacement;
        else // 否则，将replacement设为其父节点的右子节点
            p.parent.right = replacement;

        // 清除p的链接
        p.left = p.right = p.parent = null;

        // 如果p是黑色，需要修复红黑树
        if (p.color == BLACK)
            fixAfterDeletion(replacement);
    } else if (p.parent == null) { // 如果p是唯一的节点，将根设为null
        root = null;
    } else { 
      	//p的左右子树都为空
        if (p.color == BLACK)
            fixAfterDeletion(p);

        if (p.parent != null) {
            if (p == p.parent.left)
                p.parent.left = null;
            else if (p == p.parent.right)
                p.parent.right = null;
            p.parent = null;
        }
    }
}

// 删除节点后修复红黑树属性
private void fixAfterDeletion(Entry<K,V> x) {
    // 当x不是根节点并且是黑色时，循环修复
    while (x != root && colorOf(x) == BLACK) {
        if (x == leftOf(parentOf(x))) { // 如果x是其父节点的左子节点
            Entry<K,V> sib = rightOf(parentOf(x)); // 获取x的兄弟节点sib

            if (colorOf(sib) == RED) { // 如果sib为红色
                setColor(sib, BLACK); // 将sib设为黑色
                setColor(parentOf(x), RED); // 将x的父节点设为红色
                rotateLeft(parentOf(x)); // 对x的父节点进行左旋
                sib = rightOf(parentOf(x)); // 更新sib为旋转后的新兄弟节点
            }

            // 如果sib的两个子节点都是黑色
            if (colorOf(leftOf(sib)) == BLACK && colorOf(rightOf(sib)) == BLACK) {
                setColor(sib, RED); // 将sib设为红色
                x = parentOf(x); // 将x指向其父节点，继续循环
            } else {
                // 如果sib的右子节点是黑色
                if (colorOf(rightOf(sib)) == BLACK) {
                    setColor(leftOf(sib), BLACK); // 将sib的左子节点设为黑色
                    setColor(sib, RED); // 将sib设为红色
                    rotateRight(sib); // 对sib进行右旋
                    sib = rightOf(parentOf(x)); // 更新sib为旋转后的新兄弟节点
                }
                // 设置sib的颜色为其父节点的颜色
                setColor(sib, colorOf(parentOf(x)));
                setColor(parentOf(x), BLACK); // 将x的父节点设为黑色
                setColor(rightOf(sib), BLACK); // 将sib的右子节点设为黑色
                rotateLeft(parentOf(x)); // 对x的父节点进行左旋
                x = root; // 将x设为根节点，结束循环
            }
        } else { 
            // 如果x是其父节点的右子节点，镜像处理左子节点的情况
            Entry<K,V> sib = leftOf(parentOf(x)); // 获取x的兄弟节点sib

            if (colorOf(sib) == RED) { // 如果sib为红色
                setColor(sib, BLACK); // 将sib设为黑色
                setColor(parentOf(x), RED); // 将x的父节点设为红色
                rotateRight(parentOf(x)); // 对x的父节点进行右旋，与左子节点情况的左旋相对应
                sib = leftOf(parentOf(x)); // 更新sib为旋转后的新兄弟节点
            }

            if (colorOf(rightOf(sib)) == BLACK &&
                colorOf(leftOf(sib)) == BLACK) { // 如果sib的两个子节点都是黑色
                setColor(sib, RED); // 将sib设为红色
                x = parentOf(x); // 将x指向其父节点，继续循环
            } else {
                if (colorOf(leftOf(sib)) == BLACK) { // 如果sib的左子节点是黑色
                    setColor(rightOf(sib), BLACK); // 将sib的右子节点设为黑色
                    setColor(sib, RED); // 将sib设为红色
                    rotateLeft(sib); // 对sib进行左旋，与右子节点情况的右旋相对应
                    sib = leftOf(parentOf(x)); // 更新sib为旋转后的新兄弟节点
                }
                setColor(sib, colorOf(parentOf(x))); // 设置sib的颜色为其父节点的颜色
                setColor(parentOf(x), BLACK); // 将x的父节点设为黑色
                setColor(leftOf(sib), BLACK); // 将sib的左子节点设为黑色
                rotateRight(parentOf(x)); // 对x的父节点进行右旋，与左子节点情况的左旋相对应
                x = root; // 将x设为根节点，结束循环
            }
        }
    }

    setColor(x, BLACK); // 设置x为黑色
}

代码添加了详细的注释，具体的逻辑大家可以对照着红黑树的删除操作的所有情况来看。

不过即使看不懂也问题不大，只要能记住红黑树极简总结里的知识点即可。

TreeSet源码解析

TreeSet其实就是简单的包装了一下TreeMap

构造函数

/**
 * 内部包装的TreeMap
 */
private transient NavigableMap<E,Object> m;


TreeSet(NavigableMap<E,Object> m) {
    this.m = m;
}

public TreeSet() {
    this(new TreeMap<E,Object>());
}

add()

public boolean add(E e) {
    return m.put(e, PRESENT)==null;
}

add的时候会调用TreeMap的put方法来进行去重

remove

public boolean remove(Object o) {
    return m.remove(o)==PRESENT;
}

remove的时候会调用TreeMap的remove方法去删除

所以TreeSet作为一个集合 是没有很多常见的数组和集合的方法的，比如 get(int index)、indexOf()等等。